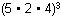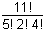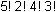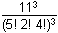Section 4: Sample Selected-Response Questions
TX PACT: Mathematics: Grades 7–12 (735)
Expand All Answers | Collapse All Answers
This section presents some sample exam questions for you to review as part of your preparation for the exam. To demonstrate how each competency may be assessed, sample questions are accompanied by the competency that they measure. While studying, you may wish to read the competency before and after you consider each sample question. Please note that the competency statements do not appear on the actual exam.
The correct answer is provided for each sample exam question. The sample questions are included to illustrate the formats and types of questions you will see on the exam; however, your performance on the sample questions should not be viewed as a predictor of your performance on the actual exam.
The following reference materials will be available to you during the exam:
Domain I—Mathematical Processes and Number Sense
Competency 001—Understand mathematical problem solving.
1. In four half-cup samples of a cereal containing dried cranberries, the numbers of cranberries were 17, 22, 22, and 18. Nutrition information on a box of this cereal defines the serving size as 1 cup or 53 grams. If a box contains 405 grams, which of the following is the best estimate of the number of cranberries in one box of this cereal?
- less than 300
- between 300 and 325
- between 326 and 350
- more than 350
- Enter to expand or collapse answer 1.Answer expanded
- Option B is correct. This question requires the examinee to analyze the use of estimation in a variety of situations (e.g., rounding, area, plausibility). There are approximately 20 cranberries per 1 half cup, or 40 cranberries per cup. The number of cups in a box is 405 divided by 53, which is approximately equal to 400 divided by 50 equals 8 (rounding both the numerator and denominator down minimizes the error). Thus the approximate number of cranberries in a box of this cereal is 8 times 40 equals 320, which is within the interval of response B.
Competency 002—Understand mathematical communication, connections, and reasoning.
2. Given statements p and q, which of the following is the truth table for the compound statement p if and only if left parenthesisq or not pright parenthesis?
-
p q p if and only if left parenthesis q or not pright parenthesis T T T T F F F T F F F F -
p q p if and only if left parenthesis q or not p right parenthesis T T T T F F F T T F F F -
p q p if and only if left parenthesis q or not p right parenthesis T T T T F F F T T F F T -
p q p if and only if left parenthesis q or not p right parenthesis T T T T F F F T F F F T
- Enter to expand or collapse answer.Answer expanded
- Option A is correct. This question requires the examinee to apply principles of logic to solve problems. First a truth value column for not p is computed as F, F, T, T (in vertical order). Then this column is used to compute truth values for the statement q or not p: T, F, T, T. Finally, this result is used to compute truth values for the full expression p if and only if left parenthesis q or not p right parenthesis: T, F, F, F.
Competency 003—Understand number theory.
3. If p and q are prime numbers and 4 over q cubed equals p squared over 50 what is the value of left parenthesis p plus q right parenthesis?
- 5
- 7
- 8
- 9
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. This question requires the examinee to apply the principles of basic number theory (e.g., prime factorization, greatest common factor, least common multiple). The variables can be isolated by multiplying both sides of the equation by 50q cubed, which yields 200 = p squared q cubed. If p and q are both prime, then p squared q cubed is the prime factorization of 200. Since 200 equals 25 times 8 equals 5 squared times 2 cubed, and 5 and 2 are both primes, p must be 5 and q must be 2, so p plus q equals 5 plus 2 equals 7.
Domain II—Patterns, Algebra, and Functions
Competency 004—Understand relations and functions.
4. Which of the following equations represents the inverse of y equals 6x minus 4 over 1 plus 3x?
- y equals x minus 4 over 3x plus 6
- y equals x pluss 4 over 6 minus 3x
- y equals 1 plus 3x over 6x minus 4
- y equals 1 minus 3xover 6x plus 4
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. This question requires the examinee to perform operations with functions, including compositions and inverses. To find the inverse of a function of the form y = f of x, the original equation is rearranged by solving it for x as a function of y: y equals 6x minus 4 over 1 plus 3x which becomes y left parenthesis 1 plus 3x right parenthesis equals 6x minus 4 which becomes y plus 3xy equals 6x minus 4 which becomes y plus 4 equals 6x minus 3xy which becomes y plus 4 equals x left parenthesis 6 minus 3y right parenthesis which becomes x equals y plus 4 over 6 minus 3y. Exchanging the variables x and y results in the inverse function f superscript negative 1, y equals x + 4 over 6 minus 3x.
Competency 005—Understand linear, quadratic, and higher-order polynomial functions.
| blank | Order 1 | Order 2 | Order 3 |
|---|---|---|---|
| soft drink | 4 | 6 | 3 |
| large pizza | 1 | 2 | 1 |
| garlic bread | 1 | 1 | 0 |
| Total Cost | 19 dollars and 62 cents | 34 dollars and 95 cents | 16 dollars and 50 cents |
5. Given the table of orders and total costs above, and that there is a solution to the problem, which of the following matrix equations could be used to find d, p, and g, the individual prices for a soft drink, a large pizza, and garlic bread respectively?
- Enter to expand or collapse answer.Answer expanded
- Option D is correct. This question requires the examinee to solve systems of linear equations or inequalities using a variety of methods. The system of linear equations can be solved using matrices. Each order can be expressed as an equation, with all three equations written with the variables in the same sequence. The first order is represented by the equation 4d plus p plus g equals 19.62, the second order by 6d plus 2p plus g equals 34.95, and the third order by 3d plus p equals 16.50. The rows of the left-hand matrix contain the coefficients of d, p, and g for each equation: left parenthesis 4 1 1 right parenthesis, left parenthesis 6 2 1 right parenthesis, and left parenthesis 3 1 0 right parenthesis. The middle matrix contains the variables, d, p, g. The right-hand matrix vertically arranges the constants of the equations.
Competency 006—Understand exponential and logarithmic functions.
6. Which of the following is equivalent to the equation 3 log base 10 x minus 2 log base 10 y equals 17?
- 3x minus 2y equals 10 to the power of 17
- x cubed minus y squared equals 10 to the power of 17
- x cubed over y squared equals 10 to the power of 17
- 3x over 2y equals 10 to the power of 17
- Enter to expand or collapse answer.Answer expanded
- Option C is correct.
This question requires the examinee to apply the laws of exponents and logarithms.
Nlog base a M equals log base a M base N which becomes 3log base 10 x equals log base 10 x cubed and 2log base 10 y equals log base 10 y squared.
Log base a M minus log base a N which becomes log base a M over N which becomes log base 10 x cubed minus log base 10 y squared equals log base 10 x cubed over y squared.
Since log base a M equals N is equivalent to a base N equals M, then log base 10 x cubed over y squared equals 17 is equivalent to 10 to the power of 17 equals x cubed over y squared.
Competency 007—Understand rational, radical, absolute value, and piece-wise defined functions.
7. Which of the following represents the domain of the function f(x) = 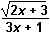 ?
?
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. This question requires the examinee to analyze rational, radical, absolute value, and piece-wise defined functions in terms of domain, range, and asymptotes. Unless otherwise specified, the domain of a function is the range of values for which the function has a real number value. A rational function must have a nonzero denominator, and solving the equation 3x plus 1 equals 0 yields x equals negative 1 third. Thus this value must be excluded from the domain. The radical expression in the numerator must have a non-negative argument and solving the inequality 2x plus 3 is greater than or equal to 0 yields x is greater than or equal to negative 3 over 2. The "or" represents the union of the two sets defined by the inequalities, or the union of the two intervals.
Domain III—Measurement and Geometry
Competency 008—Understand measurement principles and procedures.
The shape of the letter B is designed as shown below, consisting of rectangles and semicircles.
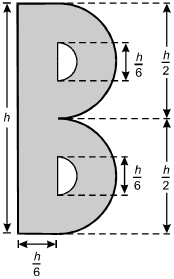
The overall height is dimensioned as h. The height of each outer semicircle is dimensioned as h over 2. The height of each semicircular void (one in the upper half of the letter and one in the lower half of the letter) is dimensioned as h over 6. The thickness of the spine of the letter is dimensioned as h over 6.
8. Which of the following formulas gives the area A of the shaded region as a function of its height h?
- A equals h squared times left parenthesis 1 over 6 plus pi over 18 right parenthesis."
- A equals h squared times left parenthesis 1 over 6 plus pi over 9 right parenthesis."
- A equals h squared times left parenthesis 1 over 6 plus 2pi over 9 right parenthesis."
- A equals h squared times left parenthesis 1 over 6 plus 5pi over 18 right parenthesis."
- Enter to expand or collapse answer.Answer expanded
- Option A is correct.
This question requires the examinee to apply the concepts of perimeter, circumference, area, surface area, and volume to solve real-world problems.
The total area of the letter B can be viewed as the area of an
h times h over 6 rectangle plus the area of a circle with radius
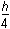 minus the area of a circle with radius
minus the area of a circle with radius
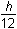 , or
h squared over 6 plus pi times the square of left parenthesis h over 4 right parenthesis squared minus pi times the square of left parenthesis h over 12 right parenthesis.
This simplifies to
h squared over 6 plus pi h squared over 16 minus pi h squared over 144. and further to
h squared times left parenthesis 1 over 6 plus pi over 16 minus pi over 144 right parenthesis. and
h squared times left parenthesis 1 over 6 plus 9pi over 144 minus pi over 144 right parenthesis and h squared times left parenthesis 1 over 6 plus pi over 18 right parenthesis.
, or
h squared over 6 plus pi times the square of left parenthesis h over 4 right parenthesis squared minus pi times the square of left parenthesis h over 12 right parenthesis.
This simplifies to
h squared over 6 plus pi h squared over 16 minus pi h squared over 144. and further to
h squared times left parenthesis 1 over 6 plus pi over 16 minus pi over 144 right parenthesis. and
h squared times left parenthesis 1 over 6 plus 9pi over 144 minus pi over 144 right parenthesis and h squared times left parenthesis 1 over 6 plus pi over 18 right parenthesis.
Competency 009—Understand Euclidean geometry in two and three dimensions.
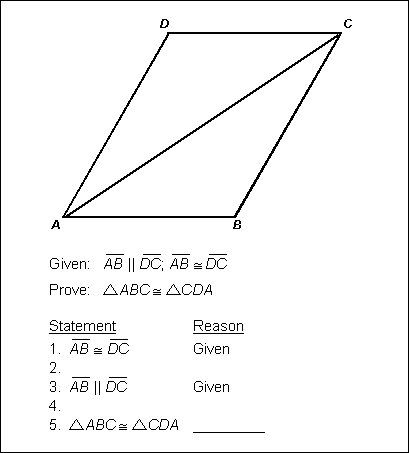
The figure is a parallelogram, ABCD. The angles at A and C are acute, and a diagonal is drawn from A to C. The proof reads as follows.
Given: Line segment AB is parallel to line segment DC, line segment A B is congruent to line segment DC.
Prove: Triangle ABC is congruent to triangle CDA.
Statement 1. Line segment AB is congruent to line segment DC. Reason, Given.
Statement 2. Blank. Reason, blank.
Statement 3. Line segment AB is parallel to line segment DC. Reason, Given.
Statement 4. Blank. Reason, blank.
Statement 5. Triangle ABC is congruent to triangle CDA. Reason, blank.
9. In the proof above, steps 2 and 4 are missing. Which of the following reasons justifies step 5?
- AAS
- ASA
- SAS
- SSS
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. This question requires the examinee to analyze formal and informal geometric proofs, including the use of similarity and congruence. The side-angle-side (SAS) theorem can be used to show that Triangle ABC and triangle CDA are congruent if each has two sides and an included angle that are congruent with two sides and an included angle of the other. In the diagram line segment AB and line segment DC are given as congruent, and the missing statement 2 is that the line segment A C is congruent to itself by the reflexive property of equality. The included angles angle BAC and angle DCA are congruent because they are alternate interior angles constructed by the transversal line segment AC that crosses the parallel line segments line segment AB and line segment DC. Thus Triangle ABC and triangle CDA meet the requirements for using SAS to prove congruence.
Competency 010—Understand coordinate and transformational geometry.
10. The vertices of triangle ABC are A left parenthesis negative 5, 3 right parenthesis, B left parenthesis 2, 2 right parenthesis, and C left parenthesis negative 1, negative 5 right parenthesis. Which of the following is the length of the median from vertex B to side AC?
- 4
- 2 times the square root of 5
- the square root of 34
- 4 times the square root of 5
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. This question requires the examinee to apply concepts of distance, midpoint, and slope to classify figures and solve problems in the coordinate plane. The midpoint of side AC where its median intersects is computed as left parenthesis negative 5 plus negative 1 over 2, 3 plus negative 5 over 2 right parenthesis equals left parenthesis negative 3, negative 1 right parenthesis. The distance from B left parenthesis 2, 2 right parenthesis to left parenthesis negative 3, negative 1 right parenthesis is computed as d equals the square root of the quantity open paren negative 3 negative 2 close paren squared plus open paren negative 1 negative 2 close paren squared equals the square root of 25 plus 9 equals the square root of 34..
Domain IV—Trigonometry and Calculus
Competency 011—Understand trigonometric functions.
11. Which of the following are the solutions to 2 sine squared theta equals cosine theta plus 1 for 0 is less than theta is less than or equal to 2pi?
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. This question requires the examinee to manipulate trigonometric expressions and equations using techniques such as trigonometric identities. Since sine squared theta equals 1 minus cosine squared theta, 2 sine squared theta equals cosine theta plus 1 which becomes 2 times 1 minus cosine squared theta equals cosine theta plus 1 which becomes 2 cosine squared theta plus cosine theta negative 1 equals 0 which becomes left parenthesis 2 cosine theta minus 1 right parenthesis times cosine theta plus 1 equals 0 which becomes cos theta equals 1 half or cosine theta equals negative 1. Thus for zero is less than theta is less than or equal to 2pi, theta equals pi over 3 comma 5pi over 3 comma or pi.
Competency 012—Understand differential calculus.
12. If f prime of x equals 3x to the fourth minus 8x squared plus 6, what is the value of the limit as h approaches 0 of f prime of left parenthesis 1 plus h right parenthesis minus f of left parenthesis 1 right parenthesis all over h?
- negative 4
- negative 1
- 1
- 4
- Enter to expand or collapse answer.Answer expanded
- Option A is correct. This question requires the examinee to analyze the derivative as the slope of a tangent line and as the limit of the difference quotient. The limit expression is equivalent to the derivative f prime of left parenthesis 1 right parenthesis. Since it is much easier to evaluate the derivative of a polynomial, this is preferred over evaluating the limit expression. f prime of x equals 12x cubed minus 16x, so f prime of 1 equals 12 minus 16 equals negative 4
Competency 013—Understand integral calculus.
13. A sum of 2000 dollars is invested in a savings account. The amount of money in the account in dollars after t years is given by the equation A equals 2000e to the 0.05t. What is the approximate average value of the account over the first two years?
- 2103 dollars
- 2105 dollars
- 2206 dollars
- 2210 dollars
- Enter to expand or collapse answer.Answer expanded
- Option A is correct. This question requires the examinee to apply integration to solve real-world problems. The average value of a continuous function f of x over an interval from a to b is 1 over b minus a times the integral from a to b of f of x d x. Since the independent variable t represents the number of years, the average daily balance over 2 years will be 1 half of the integral of the function evaluated from 0 to 2: 1 half the integral from 0 to 2 of 2000 e to the 0.05t dt equals 1000 over 0.05 times e to the 0.1 minus 1, which is approximately equal to 2103.
Domain V—Statistics, Probability, and Discrete Mathematics
Competency 014—Understand principles and techniques of statistics.
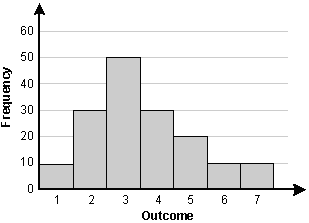
The vertical axis is labeled frequency. The horizontal axis is labeled outcome. The values of the bars are:
Outcome, 1, frequency 10
Outcome, 2, frequency 30
Outcome, 3, frequency 50
Outcome, 4, frequency 30
Outcome, 5, frequency 20
Outcome, 6, frequency 10
Outcome, 7, frequency 10
14. Which of the following statements describes the set of data represented by the histogram above?
- The mode is equal to the mean.
- The mean is greater than the median.
- The median is greater than the range.
- The range is equal to the mode.
- Enter to expand or collapse answer.Answer expanded
- Option B is correct. This question requires the examinee to analyze data in a variety of representations. The mean can be calculated as left bracket 10 left parenthesis 1 right parenthesis plus 30 left parenthesis 2 right parenthesis plus 50 left parenthesis 3 right parenthesis plus 30 left parenthesis 4 right parenthesis plus 20 left parenthesis 5 right parenthesis plus 10 left parenthesis 6 right parenthesis plus 10 left parenthesis 7 right parenthesis right bracket divided by 160 equals 3.5625. The median is the 50th percentile, which is 3. The mode is the most frequent value, which is 3. The range is 7 minus 1 equals 6. Thus "the mean is greater than the median" is the correct response.
Competency 015—Understand principles and techniques of probability.
15. The heights of adults in a large group are approximately normally distributed with a mean of 65 inches. If 20% of the adult heights are less than 62.5 inches, what is the probability that a randomly chosen adult from this group will be between 62.5 inches and 67.5 inches tall?
- 0.3
- 0.4
- 0.5
- 0.6
- Enter to expand or collapse answer.Answer expanded
- Option D is correct. This question requires the examinee to analyze uniform, binomial, and normal probability distributions. A normal distribution is symmetric about the mean. Thus if 20% of the heights are less than 62.5 inches (2.5 inches from the mean), then 20% of the heights will be greater than 67.5 inches (also 2.5 inches from the mean). Thus 100 percent minus left parenthesis 20 percent plus 20 percent right parenthesis equals 60 percent and the probability is 0.6 that the adult will be between 62.5 and 67.5 inches tall.
Competency 016—Understand principles of discrete mathematics.
16. Five different algebra textbooks, two different calculus textbooks, and four different geometry textbooks are to be arranged on a shelf. How many different arrangements are possible if the books of each subject must be kept together?
- left parenthesis 5 times 2 times 4 right parenthesis cubed
- 11 factorial over 5 factorial 2 factorial 4 factorial
- 5 factorial 2 factorial 4 factorial 3 factorial
- 11 cubed over left parenthesis 5 factorial 2 factorial 4 factorial right parenthesis cubed
- Enter to expand or collapse answer.Answer expanded
- Option C is correct. This question requires the examinee to apply concepts of permutations and combinations to solve problems. If the books in each of the 3 subjects must be kept together, then the number of ways the groups of books can be arranged by subject is represented by 3 factorial. If there are n books within a subject, the number of ways the books can be arranged is n!. Thus the algebra books can be arranged in 5 factorial different ways, the calculus books can be arranged in 2 factorial different ways, and the geometry books can be arranged in 4 factorial different ways. Since there is independence between the different arrangements computed, the total number of ways the books can be arranged is the product of all the factorials 3 factorial 5 factorial 2 factorial 4 factorial which is equivalent to 5 factorial 2 factorial 4 factorial 3 factorial.
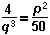
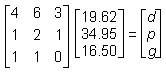
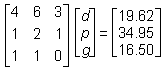
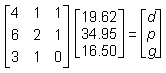
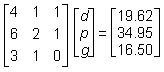
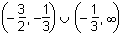
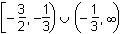
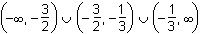
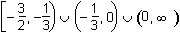
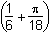
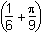
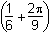
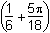
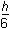
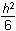 +
+ 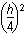 –
– 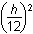 .
.
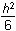 +
+
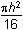 –
–
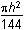
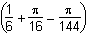
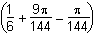 and h2
and h2
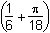 .
.
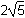
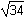
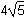
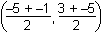 = (–3, –1)
= (–3, –1)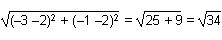
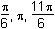
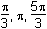
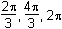
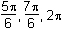
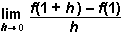
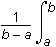 f(x)dx
f(x)dx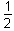
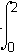 2000e0.05td t =
2000e0.05td t =
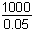 (e0.1 – 1) ≈ 2103
(e0.1 – 1) ≈ 2103